Mysteries of the World 
Pah Tum: An Ancient Game Mystery
I have long been interested in ideas and evidence hinting that conventional history may be a distortion. There are many legends and theories that say there was a golden age of humanity in the ancient past. An age where certain knowledge, technology and human spiritual prowess were in some ways much greater then they are presently.Are there traces of this ancient knowledge encoded in ancient board games-some of which are said to pre-date written language?
Are there ancient games that were specially designed to help develop the players in specific ways for example helping them to develop mentally or spiritually in some way? Perhaps some games were deliberately designed to help focus the mind on particular tactics that were useful on the battlefield and in other arenas of life.
Is it possible that advanced knowledge related to mathematics, physics or astronomy etc could be encoded in some of these ancient games? Could their study lead to a new light on the kabbalah and other esoteric topics?
Pah Tum may be one such example:
It is a two player game played on a 7x7 board with an odd number of randomly positioned blocks (or unplayable positions). The exact number of blocks used is unknown but was probably between 5 and 13 (odd numbers only). The number and position of blocks may have been determined randomly. Or perhaps a number was decided on and then each player took in turns placing a block as a pre-game set up. Alternatively player 1 may have decided the number and position of the blocks.
The goal of the game is to score more points than your opponent. The players, Black and White, take turns placing black and white stones, respectively, on the board's intersections until the entire board is completely filled.
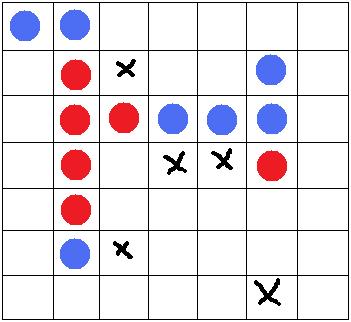
(An example of a game of Pah Tum in midplay)
Points are scored for getting 3 or more stones of your color in a row horizontally or vertically, but not diagonally. The number of points scored is:
3 in a row=3 points
4 in a row=10 points
5 in a row=25 points
6 in a row=56 points
7 in a row=119 points
I was immediately struck by the unusual scoring sequence:
3 10 25 56 119
and so I looked it up in the handy On-Line Encyclopedia of Integer Sequences:
oeis.org/?q=3%2C10%2C25%2C56%2C119
The sequence was there and it seemed to be linked to some advanced mathematics-certainly advanced for when the game was created thousands of years ago:
2^n-n-2
Ways of placing n labeled balls into 2 indistinguishable boxes with at least 2 balls in each box.
2^a(n) = integer values of the form 1/(2-sum(i=1,m, i/2^i)). - Benoit Cloitre Oct 25 2002
Number of permutations avoiding 13-2 that contain the pattern 23-1 exactly twice.
Cost of ternary maximum height Huffman tree with N internal nodes (non-leaves) for minimizing absolutely ordered sequences of size n=2N+1. - Alex Vinokur (alexvn(AT)barak-online.net), Nov 02 2004
a(n)=number of Dyck (n+3)-paths whose third upstep initiates the last long ascent, n>=1. A long ascent is one consisting of 2 or more upsteps. For example, a(1)=3 counts UUDuUDDD, UDUDuUDD, UUDDuUDD (third upstep in small type). - David Callan (callan(AT)stat.wisc.edu), Dec 08 2004
Most of these mathematics were difficult for me to understand so I made some initial enquiries:
| The formula 2^n-n-2 fits the sequence when n is greater than 1 since:-
2^1 - 1 -2 = 2 - 1 -2 = -1 2^2 - 1 -2 = 4 -2 -2 = 0 2^3 - 1 -2 = 8 - 3 -2 = 3 2^4 - 1 -2 = 16 - 4 -2 = 10 2^5 - 1 -2 = 32 -5 -2 = 25 etc... The next line 'ways of placing n labelled balls into 2 indistinguishable boxes with at least 2 balls in each box.' can be understood too, but is a bit harder. The quickest way of doing this is to use the nCr key on a calculator, but understanding how it works relies on drawing two boxes and numbered balls. Thanks to Dr Brian Williamson (http://www.drbrianwilliamson.com site down?) |
Why did the ancients use that number sequence as the basis of the Pau Tum scoring system? Is there a simple explanation or does it point to something more mysterious?
Please Contact me if you have any information about Pah Tum or mathematics related to the number sequence.
Related External Links
en.wikipedia.org/wiki/Pah_Tum
vying.org/games/pah_tum">vying.org/games/pah_tum (site down?)
vying.org/games/pah_tum/play">Play against the computer (site down?)
You are here: Home
Mysteries of the World