You are here: Home Esoteric Wisdom

Pascal's Triangle and Combinatorics

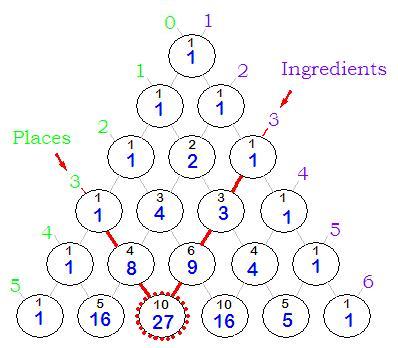
Pascal's Triangle can be used to easily work out the number of permutations for a given number of "ingredients" and "places". For example the above diagram highlights that the number of permutations for 3 ingredients over 3 places equals 27:

AAA	AAB	ABA	BAA	AAC	ACA	CAA	ABC	ACB
BBB	BBA	BAB	ABB	BBC	BCB	CBB	BCA	BAC
CCC	CCA	CAC	ACC	CCB	CCB	BCC	CAB	CBA

One simply follows the diagonals down from each side. The circle where they meet shows the answer. The smaller number in the circle indicates the number of different Ratios possible for the ingredients and places. In this case it is 10:

	ABC
AAA	BBB	CCC
AAB	BBA	CCA
AAC	BBC	CCB

Note that the small black "Ratio" numbers are identical with the numbers of Pascal's Triangle.

The larger blue "Permutation" numbers follow a simple pattern. The diagonal line from a particular Ingredient Number contains all the powers of that number from 1 to as far as the triangle is extended. For example the 2 Ingredient Line contains all the powers of 2 ie: 1,2,4,8,16,32...etc and the 3 Ingredient Line contains all the powers of 3 ie: 1, 3, 9, 27, 81...etc.

The diagnal line from a particular Place Number contains all the numbers of a particular power from 1 to as far as the triangle is extended. For example the 2 Place Line includes all the Square Numbers ie: 1, 4, 9, 16, 25...etc and the 3 Place Line contains all the cube numbers ie: 1, 8, 27, 64...etc.

You are here: Home Esoteric Wisdom