The Esoteric Section 
The n-Dimensional Simplexes and Pascal's Triangle
"Number" is not resticted to the 3 dimensions of our physical world but spans all dimensions from zero to infinity. In any dimension there is a shape which constitutes the simplest configuration.The simplest possible shape in any dimension is called an n-dimensional simplex where n denotes the number of dimensions. For example:
in 0 dimensional space the point is the simplest shape.
in 1 dimensional space the line is the simplest shape.
in 2 dimensional space the triangle is the simplest shape.
in 3 dimensional space the tetrahedon is the simplest shape.
...and so on to infinity. Of course we cannot use a different name for the simplest shape in every dimension so we use the shorthand of n-dimensional simplex.
| n-dimensional simplex | English Name |
| 0 | Point |
| 1 | Line |
| 2 | Triangle |
| 3 | Tetrahedon |
| 4 | Pentalope |
| simplex | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 4 | 6 | 4 | 1 | 0 | 0 | 0 | 0 |
| 4 | 5 | 10 | 10 | 5 | 1 | 0 | 0 | 0 |
| 5 | 6 | 15 | 20 | 15 | 6 | 1 | 0 | 0 |
| 6 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | 0 |
| 7 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
This table is a slightly modified Pascal's triangle illustrating a remarkable connection between simplices and simplex figurate numbers.
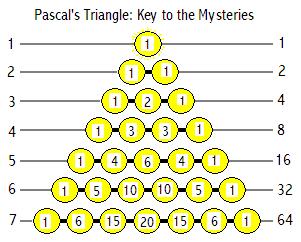
The features of a given simplex correspond exactly with a particular level of Pascal's triangle which in turn corresponds with a particular numbers' partition structure.
These partition structures can be represented with binary figures. Base 2 is the simplest possible numerical system of notation. So there is a direct relation between the simplest shape, the simplest base and ways in which a number can be partitioned.
The number of ways in which 5 can be partitioned corresponds with the Tetrahedron.
You are here: Home
The Esoteric Section