You are here: Home Conceptual Science

The Calculus of Logic

by George Boole

Cambridge and Dublin Mathematical Journal
Vol. III (1848), pp. 183-98

In a work lately published (1) I have exhibited the application of a new and peculiar form of Mathematics to the expression of the operations of the mind in reasoning. In the present essay I design to offer such an account of a portion of this treatise as may furnish a correct view of the nature of the system developed. I shall endeavour to state distinctly those positions in which its characteristic distinctions consist, and shall offer a more particular illustration of some features which are less prominently displayed in the original work. The part of the system to which I shall confine my observations is that which treats of categorical propositions, and the positions which, under this limitation, I design to illustrate, are the following:

(1) That the business of Logic is with the relations of classes, and with the modes in which the mind contemplates those relations.

(2) That antecedently to our recognition of the existence of propositions, there are laws to which the conception of a class is subject, - laws which are dependent upon the constitution of the intellect, and which determine the character and form of the reasoning process.

(3) That those laws are capable of mathematical expression, and that they thus constitute the basis of an interpretable calculus.

(4) That those laws are, furthermore, such, that all equations which are formed in subjection to them, even though expressed under functional signs, admit of perfect solution, so that every problem in logic can be solved by reference to a general theorem.

(5) That the forms under which propositions are actually exhibited, in accordance with the principles of this calculus, are analogous with those of a philosophical language.

(6) That although the symbols of the calculus do not depend for their interpretation upon the idea of quantity, they nevertheless, in their particular application to syllogism, conduct us to the quantitative conditions of inference.

It is specially of the two last of these positions that I here desire to offer illustration, they having been but partially exemplified in the work referred to. Other points will, however, be made the subjects of incidental discussion. It will be necessary to premise the following notation.

The universe of conceivable objects is represented by 1 or unity. This I assume as the primary and subject conception. All subordinate conceptions of class are understood to be formed from it by limitation, according to the following scheme.

Suppose that we have the conception of any group of objects consisting of Xs, Ys, and others, and that x, which we shall call an elective symbol, represents the mental operation of selecting from that group all the Xs which it contains, or of fixing the attention upon the Xs to the exclusion of all which are not Xs, y the mental operation of selecting the Ys, and so on; then, 1 or the universe being the subject conception, we shall have

x 1 or x = the class X,
y 1 or y = the class Y,
xy 1 or xy = the class each member of which is both X and Y,

and so on.

In like manner we shall have

1 - x = the class not-X,
1 - y = the class not-Y,
x(1 - y) = the class whose members are Xs but not-Ys,
(1 - x)(1 - y) = the class whose members are neither Xs nor Ys,
&c.

Furthermore, from consideration of the nature of the mental operation involved, it will appear that the following laws are satisfied.

Representing by x, y, z any elective symbols whatever,

x(y+z) = xy + xz	. . . . . . . .(1),
xy = yx, &c.	. . . . . . . .(2),
x = x, &c.	. . . . . . . .(3).

From the first of these it is seen that elective symbols are distributive in their operation; from the second that they are commutative. The third I have termed the index law; it is peculiar to elective symbols.

The truth of these laws does not at all depend upon the nature, or the number, or the mutual relations, of the individuals included in the different classes. There may be but one individual in a class, or there may be a thousand. There may be individuals common to different classes, or the classes may be mutually exclusive. All elective symbols are distributive, and commutative, and all elective symbols satisfy the law expressed by (3).

These laws are in fact embodied in every spoken or written language. The equivalence of the expressions ``good wise man'' and ``wise good man,'' is not a mere truism, but an assertion of the law of commutation exhibited in (2). And there are similar illustrations of the other laws.

With these laws there is connected a general axiom. We have seen that algebraic operations performed with elective symbols represent mental processes. Thus the connexion of two symbols by the sign + represents the aggregation of two classes into a single class, the connexion of two symbols xy as in multiplication, represents the mental operation of selecting from a class Y those members which belong also to another class X, and so on. By such operations the conception of a class is modified. But beside this the mind has the power of perceiving relations of equality among classes. The axiom in question, then, is that if a relation of equality is perceived between two classes, that relation remains unaffected when both subjects are equally modified by the operations above described. (A). This axiom, and not ``Aristotle's dictum,'' is the real foundation of all reasoning, the form and character of the process being, however, determined by the three laws already stated.

It is not only true that every elective symbol representing a class satisfies the index law (3), but it may be rigorously demonstrated that any combination of elective symbols 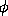(xyz..), which satisfies the law 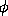(xyz..) 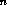= 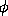(xyz..), represents an intelligible conception, - a group or class defined by a greater or less number of properties and consisting of a greater or less number of parts.

The four categorical propositions upon which the doctrine of ordinary syllogism is founded, are

All Ys are Xs.	A,
No Ys are Xs.	E,
Some Ys are Xs.	I,
Some Ys are not Xs.	O.

We shall consider these with reference to the classes among which relation is expressed.

A. The expression All Ys represents the class Y and will therefore be expressed by y, the copula are by the sign =, the indefinite term, Xs, is equivalent to Some Xs. It is a convention of language, that the word Some is expressed in the subject, but not in the predicate of a proposition. The term Some Xs will be expressed by vx, in which v is an elective symbol appropriate to a class V, some members of which are Xs, but which is in other respects arbitrary. Thus the proposition A will be expressed by the equation

y = vx . . . . . . . .(4).

E. (2) In the proposition, No Ys are Xs, the negative particle appears to be attached to the subject instead of to the predicate to which it manifestly belongs. We do not intend to say that those things which are not-Ys are Xs, but that things which are Ys are not-Xs. Now the class not-Xs is expressed by 1 - x; hence the proposition No Ys are Xs, or rather All Ys are not-Xs, will be expressed by

y = v(1 - x) . . . . . . . .(5).

I. In the proposition Some Ys are Xs, or Some Ys are Some Xs, we might regard the Some in the subject and the Some in the predicate as having reference to the same arbitrary class V, and so write

vy = vx,

but it is less of an assumption to refrain from doing this. Thus we should write

vy = v'x . . . . . . . .(6),

v' referring to another arbitrary class V'.

O. Similarly, the proposition Some Ys are not-Xs, will be expressed by the equation

vy = v'(1 - x) . . . . . . . .(7).

It will be seen from the above that the forms under which the four categorical propositions A, E, I, O are exhibited in the notation of elective symbols are analogous with those of pure language, i.e. with the forms which human speech would assume, were its rules entirely constructed upon a scientific basis. In a vast majority of the propositions which can be conceived by the mind, the laws of expression have not been modified by usage, and the analogy becomes more apparent, e.g. the interpretation of the equation

z = x(1 - y) + y(1 - x),

is, the class Z consists of all Xs which are not-Ys and of all Ys which are not-Xs.

General Theorems relating to Elective Functions.

We have now arrived at this step, - that we are in possession of a class of symbols x, y, z, &c. satisfying certain laws, and applicable to the rigorous expression of any categorical proposition whatever. It will be our next business to exhibit a few of the general theorems of the calculus which rest upon the basis of those laws, and these theorems we shall afterwards apply to the discussion of particular examples.

Of the general theorems I shall only exhibit two sets: those which relate to the development of functions, and those which relate to the solution of equations.

Theorems of Development.

(1) If x be any elective symbol, then

(x) = (1) x + (0) (1 - x) . . . . . . . .(8),

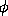the coefficients (1), 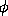(0), which are quantitative or common algebraic functions, are called the moduli, and x and 1 - x the constituents.

(2) For a function of two elective symbols we have

(xy) = (11)xy + (10) x(1 - y)
       + (01)(1 - x)y + (00)(1 - x)(1 - y) . . . . . . . .(9),

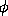in which (11), 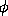(10), &c. are quantitative, and are called the moduli, and xy, x(1 - y), &c. the constituents.

(3) Functions of three symbols:

(xyz) = (111)xyz + (110)xy(1 - z)
       + (101)x(1 - y)z + (100)x(1 - y)(1 - z)
       + (011)(1 - x)yz + (010)(1 - x)y(1 - z)
       + (001)xy(1 - z) + (000)(1 - x)(1 - y)(1 - z) . . . . . . . .(10),

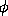in which (111), 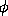(110), &c. are the moduli, and xyz, xy(1 - z), &c. the constituents.

From these examples the general law of development is obvious. And I desire it to be noted that this law is a mere consequence of the primary laws which have been expressed in (1), (2), (3).

THEOREM. If we have any equation 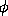(xyz..) = 0, and fully expand the first member, then every constituent whose modulus does not vanish may be equated to 0.

This enables us to interpret any equation by a general rule.

RULE. Bring all the terms to the first side, expand this in terms of all the elective symbols involved in it, and equate to 0 every constituent whose modulus does not vanish.

For the demonstration of these and many other results, I must refer to the original work. It must be noted that on p. 66, z has been, through mistake, substituted for w, and that the reference on p. 80 should be to Prop. 2.

As an example, let us take the equation

x + 2y - 3xy = 0 . . . . . . . .(11).

Here 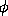(xy) = x + 2y - 3xy, whence the values of the moduli are

(11) = 0,   (10) = 1,   (01) = 2,   (00) = 0,

so that the expansion (9) gives

x(1 - y) + 2y(1 - x) = 0,

which is in fact only another form of (11). We have, then, by the Rule

x(1 - y) = 0 . . . . . . . .(11),
y(1 - x) = 0 . . . . . . . .(12);

the former implies that there are no Xs which are not-Ys, the latter that there are no Ys which are not-Xs, these together expressing the full significance of the original equation.

We can, however, often recombine the constituents with a gain of simplicity. In the present instance, subtracting (12) from (11), we have x - y = 0, or x = y, that is, the class X is identical with the class Y. This proposition is equivalent to the two former ones.

All equations are thus of equal significance which give, on expansion, the same series of constituent equations, and all are interpretable.

General Solution of Elective Equations.

(1) The general solution of the equation 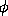(xy) = 0, in which two elective symbols only are involved, y being the one whose value is sought, is

The coefficients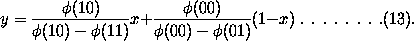

are here the moduli.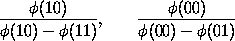

(2) The general solution of the equation 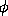(xyz) = 0, z being the symbol whose value is to be determined, is

the coefficients of which we shall still term the moduli. The law of their formation will readily be seen, so that the general theorems which have been given for the solution of elective equations of two and three symbols, may be regarded as examples of a more general theorem applicable to all elective equations whatever. in applying these results it is to be observed, that if a modulus assume the form 0/0 it is to be replaced by an arbitrary elective symbol w, and that if a modulus assume any numerical value except 0 or 1, the constituent of which it is a factor must be separately equated to 0. Although these conditions are deduced solely from the laws to which the symbols are obedient, and without any reference to interpretation, they nevertheless render the solution of every equation interpretable in logic. To such formulae also every question upon the relations of classes may be referred. One or two very simple illustrations may suffice.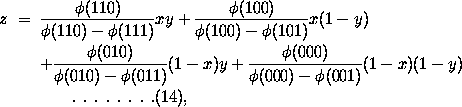

(1) Given yx = yz + x(1 - z) . . . . . . . . (a).
The Ys which are Xs consist of the Ys which are Zs and the Xs which are not-Zs. Required the class Z.

Here 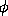(xyz) = yx - yz - x(1 - z),

(111) = 0,   (110) = 0,   (101) = 0,
(100) = -1,   (011) = -1,   (010) = 0,
(001) = 0,   (000) = 0;

and substituting in (14), we have

z = 0/0 xy + x(1 - y) + 0/0 (1 - x)(1 - y)
  = x(1 - y) + wxy + w'(1 - x)(1 - y) . . . . . . . .(15).

(3) Hence the class Z includes all Xs which are not-Ys, an indefinite number of Xs which are Ys, and an indefinite number of individuals which are neither Xs nor Ys. The classes w and w' being quite arbitrary, the indefinite remainder is equally so; it may vanish or not.

Since 1 - z represents a class, not-Z, and satisfies the index law

(1 - z) = 1 - z,

as is evident on trial, we may, if we choose, determine the value of this element just as we should determine that of z.

Let us take, in illustration of this principle, the equation y = vx, (All Ys are Xs), and seek the value of 1 - x, the class not-X.

Put 1 - x = z then y = v(1 - z), and if we write this in the form y - v(1 - z) = 0 and represent the first member by 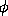(vyz), v here taking the place of x, in (14), we shall have

(111) = 1,   (110) = 0,   (101) = 0,   (100) = -1,
(011) = 1,   (010) = 1,   (001) = 0,   (000) = 0;

the solution will thus assume the form

or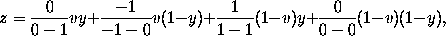

1 - x = v(1 - y) + 1/0 (1 - v)y + 0/0 (1 - v)(1 - y) . . . . . . . .(16).

The infinite coefficient of the second term in the second member permits us to write

y(1 - v) = 0 . . . . . . . .(17),

the coefficient 0/0 being then replaced by w, an arbitrary elective symbol, we have

1 - x = v(1 - y) + w(1 - v)(1 - y),

or

1 - x = {v + w(1 - v)} (1 - y) . . . . . . . .(18).

We may remark upon this result that the coefficient v + w(1 - v) in the second member satisfies the condition

{v + w(1 - v)} = v + w(1 - v),

as is evident on squaring it. It therefore represents a class. We may replace it by an elective symbol u, we have then

1 - x = u(1 - y) . . . . . . . .(19),

the interpretation of which is

All not-Xs are not-Ys.

This is a known transformation in logic, and is called conversion by contraposition, or negative conversion. But it is far from exhausting the solution we have obtained. Logicians have overlooked the fact, that when we convert the proposition All Ys are (some) Xs into All not-Xs are (some) not-Ys there is a relation between the two (somes), understood in the predicates. The equation (18) shews that whatever may be that condition which limits the Xs in the original proposition, - the not-Ys in the converted proposition consist of all which are subject to the same condition, and of an arbitrary remainder which are not subject to that condition. The equation (17) further shews that there are no Ys which are not subject to that condition.

We can similarly reduce the equation y = v(1 - x), No Ys are Xs, to the form x = v'(1 - y) No Xs are Ys, with a like relation between v and v'. If we solve the equation y = vx All Ys are Xs, with reference to v, we obtain the subsidiary relation y(1 - x) = 0 No Ys are not-Xs, and similarly from the equation y = v(1 - x) (No Ys are Xs) we get xy = 0. These equations, which may also be obtained in other ways, I have employed in the original treatise. All equations whose interpretations are connected are similarly connected themselves, by solution or development.

On Syllogism.

The forms of categorical propositions already deduced are

y = vx,	All Ys are Xs,
y = v(1 - x),	No Ys are Xs,
vy = v'x,	Some Ys are Xs,
vy = v'(1 - x),	Some Ys are not-Xs,

whereof the two first give, by solution, 1 - x = v'(1 - y). All not-Xs are not-Ys, x = v'(1 - y), No Xs are Ys. To the above scheme, which is that of Aristotle, we might annex the four categorical propositions

1 - y = vx,	All not-Ys are Xs,
1 - y = v(1 - x),	All not-Ys are not-Xs,
v(1 - y) = v'x,	Some not-Ys are Xs,
v(1 - y) = v'(1 - x),	Some not-Ys are not-Xs,

the first two of which are similarly convertible into

1 - x = v'y,		All not-Xs are Ys,
x = v'y,		All Xs are Ys,
	or	No not-Xs are Ys,

If now the two premises of any syllogism are expressed by equations of the above forms, the elimination of the common symbol y will lead us to an equation expressive of the conclusion.

Ex. 1.	All Ys are Xs,	y = vx,
	All Zs are Ys,	z = v'y,

the elimination of y gives

z = vv'x,

the interpretation of which is

All Zs are Xs,

the form of the coefficient vv' indicates that the predicate of the conclusion is limited by both the conditions which separately limit the predicates of the premises.

Ex. 2.	All Ys are Xs,	y = vx,
	All Ys are Zs,	y = v'z.

The elimination of y gives

v'z = vx,

which is interpretable into Some Zs are Xs. It is always necessary that one term of the conclusion should be interpretable by means of the equations of the premises. In the above case both are so.

Ex. 3.	All Xs are Ys,	x = vy,
	No Zs are Ys,	z = v'(1 - y).

Instead of directly eliminating y let either equation be transformed by solution as in (19). The first gives

1 - y = u(1 - x),

u being equivalent to v + w(1 - v), in which w is arbitrary. Eliminating 1 - y between this and the second equation of the system, we get

z = v'u(1 - x),

the interpretation of which is

No Zs are Xs.

Had we directly eliminated y, we should have had

vz = v'(v - x),

the reduced solution of which is

z = v'{v + (1 - v)}(1 - x),

in which w is an arbitrary elective symbol. This exactly agrees with the former result.

These examples may suffice to illustrate the employment of the method in particular instances. But its applicability to the demonstration of general theorems is here, as in other cases, a more important feature. I subjoin the results of a recent investigation of the Laws of Syllogism. While those results are characterized by great simplicity and bear, indeed, little trace of their mathematical origin, it would, I conceive, have been very difficult to arrive at them by the examination and comparison of particular cases.

Laws of Syllogism deduced from the Elective Calculus.

We shall take into account all propositions which can be made out of the classes X, Y, Z, and referred to any of the forms embraced in the following system,

A,	All Xs are Zs.	A',	All not-Xs are Zs.
E,	No Xs are Zs.	E'	No not-Xs are Zs, or
			(All not-Xs are not-Zs.)
I,	Some Xs are Zs.	I',	Some not-Xs are Zs.
O,	Some Xs are not-Zs.	O',	Some not-Xs are not-Zs.

It is necessary to recapitulate that quantity (universal and particular) and quality (affirmative and negative) are understood to belong to the terms of propositions (4) which is indeed the correct view.

Thus, in the proposition All Xs are Ys, the subject All Xs is universal-affirmative, the predicate (some) Ys particular-affirmative.

In the proposition, Some Xs are Zs, both terms are particular-affirmative.

The proposition No Xs are Zs would in philosophical language be written in the form All Xs are not-Zs. The subject is universal-affirmative, the predicate particular-negative.

In the proposition Some Xs are not-Zs, the subject is particular-affirmative, the predicate particular-negative. In the proposition All not-Xs are Ys the subject is universal-negative, the predicate particular-affirmative, and so on.

In a pair of premises there are four terms, viz. two subjects and two predicates; two of these terms, viz. those involving the Y or not-Y may be called the middle terms, the two others the extremes, one of these involving X or not-X, the other Z or not-Z.

The following are then the conditions and the rules of inference.

Case 1st. The middle terms of like quality.

Condition of Inference. One middle term universal.

Rule. Equate the extremes.

Case 2nd. The middle terms of opposite qualities.

1st. Condition of Inference. One extreme universal.

Rule. Change the quantity and quality of that extreme, and equate the result to the other extreme.

2nd. Condition of inference. Two universal middle terms.

Rule. Change the quantity and quality of either extreme, and equate the result to the other extreme.

I add a few examples,

1st	All Ys are Xs.
	All Zs are Ys.

This belongs to Case 1. All Ys is the universal middle term. The extremes equated give All Zs are Xs, the stronger term becoming the subject.

2nd	All Xs are Ys	=	All Xs are Ys
	No Zs are Ys		No Zs are not-Ys

This belongs to Case 2, and satisfies the first condition. The middle term is particular-affirmative in the first premise, particular-negative in the second. Taking All-Zs as the universal extreme, we have, on changing its quantity and quality, Some not-Zs, and this equated to the other extreme gives

All Xs are (some) not-Zs = No Xs are Zs.

If we take All Xs as the universal extreme we get

No Zs are Xs.

3rd	All Xs are Ys.
	Some Zs are not-Ys.

This also belongs to Case 2, and satisfies the first condition. The universal extreme All Xs becomes, some not-Xs, whence

Some Zs are not-Xs.

4th	All Ys are Xs.
	All not-Ys are Zs.

This belongs to Case 2, and satisfies the second condition. The extreme Some Xs becomes All not-Xs,

.·. All not-Xs are Zs.

The other extreme treated in the same way would give

All not-Zs are Xs,

which is an equivalent result.

If we confine ourselves to the Aristotelian premises A, E, I, O, the second condition of inference in Case 2 is not needed. The conclusion will not necessarily be confined to the Aristotelian system.

Ex.	Some Ys are not-Xs	=	Some Ys are not-Xs
	No Zs are Ys		All Zs are not-Ys

This belongs to Case 2, and satisfies the first condition. The result is

Some not-Zs are not-Xs.

These appear to me to be the ultimate laws of syllogistic inference. They apply to every case, and they completely abolish the distinction of figure, the necessity of conversion, the arbitrary and (5) rules of distribution, &c. If all logic were reducible to the syllogism these might claim to be regarded as the rules of logic. But logic, considered as the science of the relations of classes has been shewn to be of far greater extent. Syllogistic inference, in the elective system, corresponds to elimination. But this is not the highest in the order of its processes. All questions of elimination may in that system be regarded as subsidiary to the more general problem of the solution of elective equations. To this problem all questions of logic and of reasoning, without exception, may be referred. For the fuller illustrations of this principle I must however refer to the original work. The theory of hypothetical propositions, the analysis of the positive and negative elements, into which all propositions are ultimately resolvable, and other similar topics are also there discussed.

Undoubtedly the final aim of speculative logic is to assign the conditions which render reasoning possible, and the laws which determine its character and expression. The general axiom (A) and the laws (1), (2), (3), appear to convey the most definite solution that can at present be given to this question. When we pass to the consideration of hypothetical propositions, the same laws and the same general axiom which ought perhaps also to be regarded as a law, continue to prevail; the only difference being that the subjects of thought are no longer classes of objects, but cases of the coexistent truth or falsehood of propositions. Those relations which logicians designate by the terms conditional, disjunctive, &c., are referred by Kant to distinct conditions of thought. But it is a very remarkable fact, that the expressions of such relations can be deduced the one from the other by mere analytical process. From the equation y = vx, which expresses the conditional proposition, ``If the proposition Y is true the proposition X is true,'' we can deduce

yx + (1 - y)x + (1 - y)(1 - x) = 1,

which expresses the disjunctive proposition, ``Either Y and X are together true, or X is true and Y is false, or they are both false,'' and again the equation y(1 - x) = 0, which expresses a relation of coexistence, viz. that the truth of Y and the falsehood of X do not coexist. The distinction in the mental regard, which has the best title to be regarded as fundamental, is, I conceive, that of the affirmative and the negative. From this we deduce the direct and the inverse in operations, the true and the false in propositions, and the opposition of qualities in their terms.

The view which these enquiries present of the nature of language is a very interesting one. They exhibit it not as a mere collection of signs, but as a system of expression, the elements of which are subject to the laws of the thought which they represent. That those laws are as rigorously mathematical as are the laws which govern the purely quantitative conceptions of space and time, of number and magnitude, is a conclusion which I do not hesitate to submit to the exactest scrutiny.

---

Notes
(1) The Mathematical Analysis of Logic, being an Essay towards a Calculus of Deductive Reasoning. Cambridge, Macmillan; London, G. Bell.

---

(2) There are but two ways in which the proposition, No Xs are Ys, can be understood. 1st, In the sense of All Xs are not-Y. 2nd, In the sense of It is not true that any Xs are Ys, i.e. the proposition ``Some Xs are Ys'' is false. The former of these is a single categorical proposition. The latter is an assertion respecting a proposition, and its expression belongs to a distinct part of the elective system. It appears to me that it is the latter sense, which is really adopted by those who refer the negative, not, to the copula. To refer it to the predicate is not a useless refinement, but a necessary step, in order to make the proposition truly a relation between classes. I believe it will be found that this step is really taken in the attempts to demonstrate the Aristotelian rules of distribution.

The transposition of the negative is a very common feature of language. Habit renders us almost insensible to it in our own language, but when in another language the same principle is differently exhibited, as in the Greek, for , it claims attention.

---

(3) This conclusion may be illustrated and verified by considering an example such as the following.

Let	x denote all steamers, or steam-vessels,
	y denote all armed vessels,
	z denote all vessels of the Mediterranean.

Equation (a) would then express that armed steamers consist of the armed vessels of the Mediterranean and the steam-vessels not of the Mediterranean. From this it follows -

(1) That there are no armed vessels except steamers in the Mediterranean.

(2) That all unarmed steamers are in the Mediterranean (since the steam-vessels not of the Mediterranean are armed). Hence we infer that the vessels of the Mediterranean consist of all unarmed steamers; any number of armed steamers; and any number of unarmed vessels without steam. This, expressed symbolically, is equation (15).

---

(4) When propositions are said to be affected with quantity and quality, the quality is really that of the predicate, which expresses the nature of the assertion, and the quantity that of the subject, which shews its extent.

---

(5) Partial, because they have reference only to the quantity of the X, even when the proposition relates to the not-X. It would be possible to construct an exact counterpart to the Aristotelian rules of syllogism, by quantifying only the not-X. The system in the text is symmetrical because it is complete.

---

You are here: Home Conceptual Science